Math is a happy place...
The words alone evoke a wide range of emotional reactions. Some people might shrug and say "Sure, why not? Whatever floats your boat". Others might even strongly agree and think that doing math problems is a good time. However, it is most likely that the title of this blog is met with a mix of skepticism, disbelief, or even down-right disgust that 'math' and 'happy' would be used in the same sentence.
While many people may not understand exactly why the thought of mathematics evokes such a negative emotional response, no one would argue that it does. Close your eyes and imagine that you're standing in front of a group of people. Now imagine you're told that you're going to be given a grade 9 math problem and that you have a minute to solve it in front of the audience. I can almost feel your body tensing up and your anxiety level rise. Yet, it is likely that if you're reading this, then you have already passed grade 9 math. What makes us so defensive about not remembering? What prevents us from wanting to take that risk and dive into the problem?
It isn't because people don't think math is important, it is actually the contrary. People know that mathematical thinking as they see it in the world is very important but feel that their experiences with it have been so disconnected. As a society, we think math is important enough to make it a compulsory subject from K-12 in school, yet we haven't figured out a way to make it compelling.
Everyone has a relationship with mathematics. Although our individual experiences vary, our collective experiences are likely more similar than they are different. As kids, we learn about patterns and numbers, get to play with blocks, and learn to count. As we get older, we learn about operations and how to do them - if we're lucky, we get to make sense of these operations, maybe even get to draw pictures about them. Then come the rules - negative times negative is positive, bedmas, find a common denominator to add fractions (but not to multiply them), powers with the same base means you add the exponents (except when you have an exponent of a power), and so on and so on. If you were a good student, then you could remember these rules enough to perform on the next test. This approach works until one day it doesn't... and all of these disconnected rules fall apart. Our brains are not built to remember disconnected facts and rules without context or meaning behind them. Yet, what I have described would be an accurate depiction of our experiences with mathematics in school from K-12, what I like to call "school math".
It is important for me to distinguish between "school math" and "mathematics" because they are so extremely different. The mathematics that we see around us being used by doctors, artists, engineers, environmentalists, and musicians looks nothing like the worksheets, textbooks, and examples that we were exposed to in school. Yet, Language Arts classrooms are filled with reading, writing, and communicating - acts that resemble the use of the language in the world around us. Same goes for science, economics, art, physical education, and almost every other class in school - they have a resemblance to those fields. So why is math so different?
Welcome to my blog. I will be dedicating the next little while writing thoughts and wonderings about that exact question. I will be offering ideas on how we can shift "school math" to be more connected, relevant, curious, interesting, and FUN so perhaps less and less people will have a negative reaction to the title "Math is a happy place".
While many people may not understand exactly why the thought of mathematics evokes such a negative emotional response, no one would argue that it does. Close your eyes and imagine that you're standing in front of a group of people. Now imagine you're told that you're going to be given a grade 9 math problem and that you have a minute to solve it in front of the audience. I can almost feel your body tensing up and your anxiety level rise. Yet, it is likely that if you're reading this, then you have already passed grade 9 math. What makes us so defensive about not remembering? What prevents us from wanting to take that risk and dive into the problem?
It isn't because people don't think math is important, it is actually the contrary. People know that mathematical thinking as they see it in the world is very important but feel that their experiences with it have been so disconnected. As a society, we think math is important enough to make it a compulsory subject from K-12 in school, yet we haven't figured out a way to make it compelling.
Everyone has a relationship with mathematics. Although our individual experiences vary, our collective experiences are likely more similar than they are different. As kids, we learn about patterns and numbers, get to play with blocks, and learn to count. As we get older, we learn about operations and how to do them - if we're lucky, we get to make sense of these operations, maybe even get to draw pictures about them. Then come the rules - negative times negative is positive, bedmas, find a common denominator to add fractions (but not to multiply them), powers with the same base means you add the exponents (except when you have an exponent of a power), and so on and so on. If you were a good student, then you could remember these rules enough to perform on the next test. This approach works until one day it doesn't... and all of these disconnected rules fall apart. Our brains are not built to remember disconnected facts and rules without context or meaning behind them. Yet, what I have described would be an accurate depiction of our experiences with mathematics in school from K-12, what I like to call "school math".
It is important for me to distinguish between "school math" and "mathematics" because they are so extremely different. The mathematics that we see around us being used by doctors, artists, engineers, environmentalists, and musicians looks nothing like the worksheets, textbooks, and examples that we were exposed to in school. Yet, Language Arts classrooms are filled with reading, writing, and communicating - acts that resemble the use of the language in the world around us. Same goes for science, economics, art, physical education, and almost every other class in school - they have a resemblance to those fields. So why is math so different?
Welcome to my blog. I will be dedicating the next little while writing thoughts and wonderings about that exact question. I will be offering ideas on how we can shift "school math" to be more connected, relevant, curious, interesting, and FUN so perhaps less and less people will have a negative reaction to the title "Math is a happy place".
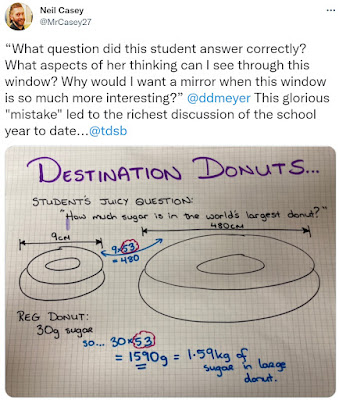
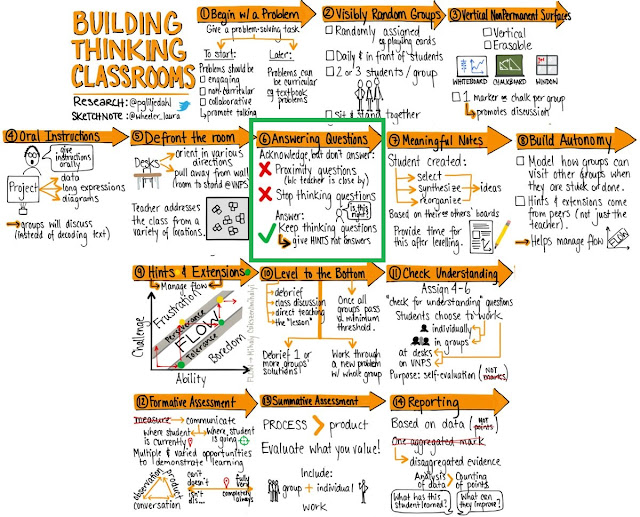
Congratulations on your new blog! It is great to see you starting this conversation. Looking forward to reading more from you, Lam. It is a wonderful mission to help everyone see that they, too, can be happy mathies.
ReplyDelete