Learning Through Mistakes

People often say that we should learn from our mistakes—that reflecting on past actions can guide our future decisions. It would be nice though rather than to reflect and learn from past mistakes (when it is often too late) that we learn through our mistakes as they are happening.

I came across a tweet recently that made me think of how to foster this in a classroom.

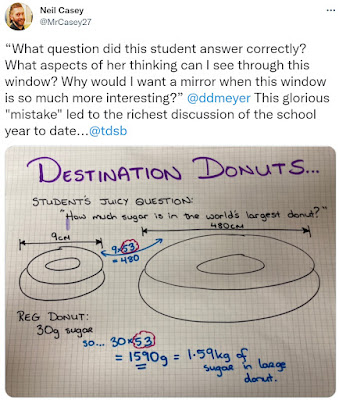
A few things jump out at me here:

It looks like the question was made by the student and while it is fun, it wouldn’t be considered a real-world application problem. This shows that problems don’t need to be useful to be relevant. This is a non-routine problem that invites mathematical thinking, and for learners to start seeing that as useful is already a win. It likely isn’t a big leap for this student to see how the thinking involved to solve this problem is valuable in many ways. I think we often get too caught up in trying to answer, “when will we ever use this?” by trying to find specific applications for the mathematics rather than focus on the mathematical thinking being developed. Putting a contrived context around some numbers and operations doesn’t make a routine problem more interesting.

The author of the tweet mentions the “mistakes” in the student thinking. Even the act of looking over the work to find the mistake was fun for me. There are some parts of the solution that are correct, but the mistakes are what led to the rich discussion (which I wish I was there to see!). I have developed such a love for student thinking over the years—when we create space for it, there are always surprises, resourcefulness, comedy, and just overall ingenuity. This occurs when our goal isn’t for students to mimic our thinking as teachers, or “hold up a mirror” as the author claims—a “window” is far more interesting.

I’ve worked hard to foster this type of space for years—a space that is truly centred on the students. This goes beyond getting to know them as learners, or designing experiences to fit their needs—it has to include their voice and their thinking. This comes with a warning: truly valuing and accepting student ideas will lead to some dead ends and mistakes.

   

A colleague of mine once came to me with a concern as he had noticed that every time he walked by my room, it looked like the students were explaining ideas to each other. “They are just developing their understanding, what if they explain things wrong? It will confuse them.”

I think we too often see confusion as a negative state. Yes, it is uncomfortable—but people often emerge from a state of confusion much more confident in their understanding than being given a clear path. When we can see the space around a concept, what works and what doesn’t, it gives us a more robust understanding of that concept. I’ve always believed that it is just as important to define an idea by not only describing what it is, but also what it is not.

I continue to refer to this Ted Talk from Dan Finkel on five principles for extraordinary math teaching, but he says it best through one of his principles: say yes to student ideas.

“Saying yes is not the same thing as saying you’re right. You can accept ideas, even wrong ideas, into the debate and say ‘yes’ to your students right to participate in the act of thinking mathematically. To have your idea dismissed out of hand is disempowering. To have it accepted, studied, and disproven is a mark of respect. It’s also more convincing to be shown you’re wrong by your peers than told you’re wrong by the teacher.”

Consider why teachers might dismiss student thinking—like my colleague, they may be fearful of causing confusion, or they dismiss student ideas in favour of a more efficient approach, or because student thinking often does not adhere to accepted terminology or conventions, or the teacher themselves are fearful of exploring ideas that they are not familiar with.

As I mentioned, confusion can be a positive state for students to work through.

Efficiency is overrated and does not resemble mathematical thinking outside of school math contexts.

Terminology and conventions are much more likely to be accepted and remembered by students when they come after the mathematical thinking experience.

And teachers positioning themselves as learners does not diminish their expertise—rather it paints a more accurate picture of what a mathematician does (when they don’t know what to do).

I’ve often thought about mathematics as a school subject and how little it resembles mathematical thinking by people using and studying mathematics for interest and for work. Problems are rarely neatly packaged as they are in school and they often take a very long time to solve (speed and efficiency are less relevant). Even precision is less important when math is being used to represent abstract models or in statistics. I don’t believe other school subjects have such a wide disconnect—at least ELA courses have opportunities for learners to engage in writing and creating. I don’t think many high school students would identify themselves as able to create and contribute new mathematical ideas.

I remember years ago, a student ran up to me with a problem he couldn’t solve and I said “I don’t know. Let’s sit down and find out.” He was so perplexed that I did not already have a clear path solution that he just left and said he would look up the answer online. We have to normalize saying “Let’s find out”, digging into a problem, making a bunch of mistakes along the way and learning through them—its what mathematicians do.